Big-O Notasyonu, algoritma analizindeki zaman karmaşıklığında üst sınırı tanımlayan, matematiksel bir gösterimdir. Algoritmanın büyüme hızını temsil etmek için kullanılır.

Algoritma analizinin dışında, matematiktsel anlamda da genellikle kırpılmış bir sonsuz serinin kalan terimini karakterize etmek için kullanılır. İlk olarak Alman matematikçi Paul Bachmann tarafından 1892 yılında kullanılmıştır. Yaygınlaşması Edmund Landau tarafından sağlanmıştır.

Big-O Notasyonu Avantajları

Big-O Notasyonu nun belli başlı avantajları vardır. Algoritma analizlerinde derleyici, donanım, bellek hızı gibi etkenlerden dolayı, belirli bir komutun çalışma süresi farklılık gösterebilmektedir.  Amacı, bu etkenlerden bağımsız bir şekilde algoritmanın verimliliğini ölçmektir. Big-O Notasyonu ile algoritmadaki sabitler ve diğer gereksiz etmenler göz ardı edilir ve analizi daha da basit bir hale getirilir.

Bazı Big-O Notasyonu Karmaşıklıkları

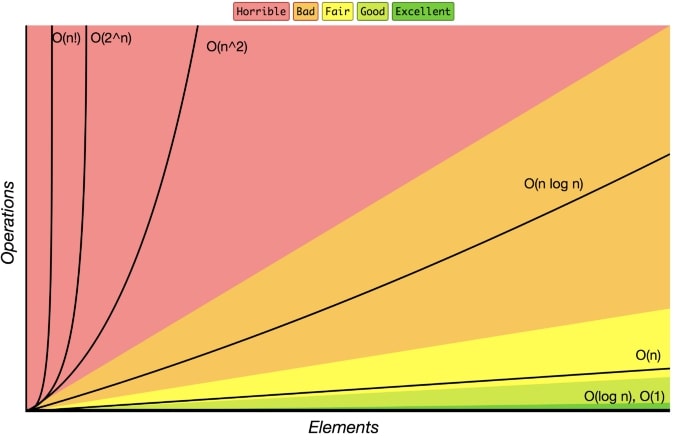
Sık karşılaştığımız Big-O karmaşıklıkları şunlardır:

• O(1) → Sabit Karmaşıklık
• O(N) → Doğrusal Karmaşıklık
• O(N²) → İkinci Dereceden Karmaşıklık
• O(logN) → Logaritmik Karmaşıklık
• O(NlogN) → Linearitmik Karmaşıklık
• O(2^N)→ Üstel Karmaşıklık
• O(N!) → Faktöriyel Karmaşıklığı

 

Burada N, veri setinin büyüklüğü ya da eleman sayısı iken c, sabit bir değerdir.

Kaynak: https://www.serkanseker.com/tr/wp-content/uploads/2021/09/big-o-karmasiklik-grafigi.jpg

 

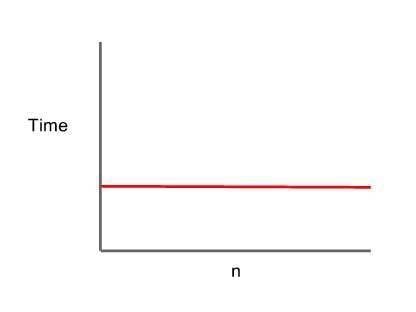
1) Sabit Karmaşıklık-O(1)

Sabit karmaşıklıkta algoritmaya girilen veri seti ne kadar büyük olursa olsun çalışma zamanı ve kullanılan kaynak miktarı sabittir.

• O(1) zamanda çalışır.

Kaynak: https://www.serkanseker.com/tr/wp-content/uploads/2021/09/Sabit-Big-O-Karmasikligi.jpg

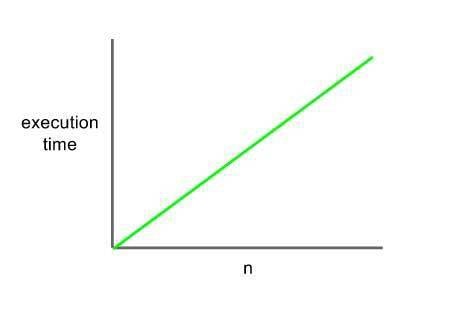
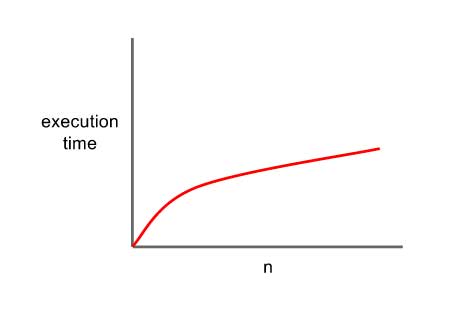
2) Doğrusal Karmaşıklık-O(N)

Doğrusal karmaşıklıkta algoritmaya girdiğimiz veri setinin büyüklüğü arttıkça çalışma zamanı da doğrusal olarak artar. Yani girilen veri setinin büyüklüğü ile çalışma zamanı arasında doğru orantı vardır.

• O(N) zamanda çalışır.

Kaynak: https://www.serkanseker.com/tr/wp-content/uploads/2021/09/Dogrusal-Big-O-Karmasikligi.jpg

 

3) İkinci Dereceden Karmaşıklık-O(N²)

Basitçe, çalışma zamanı girdi büyüklüğünün karesiyle doğru orantılıdır. Yani eğer girdi büyüklüğü 2 ise 4 işlem, 8 ise 16 işlem gerçekleşir.

• O(N²) zamanda çalışır.

Kaynak: https://www.serkanseker.com/tr/wp-content/uploads/2021/09/Quadratic-Big-O-Karmasikligi.jpg

 

4) Logaritmik Karmaşıklık-O(log N)

Logaritmik karmaşıklık genel olarak her seferinde problemi ikiye bölen algoritmalarda karşımıza çıkar. Diğer bir deyişle, algoritmayı çalıştırmak için geçen süre N girdi boyutunun logaritması ile orantılıysa bu algoritma logaritmik zaman karmaşıklığına sahiptir.

• O(logN) zamanda çalışır.

Kaynak: https://www.serkanseker.com/tr/wp-content/uploads/2021/09/Logaritmik-Big-O-Karmasikligi.jpg

 

5) Linearitmik Karmaşıklık-O(NlogN)

Linearitmik zaman karmaşıklığı, doğrusal bir algoritmadan biraz daha yavaştır, ancak yine de ikinci dereceden bir algoritmadan çok daha iyidir.

• O(NlogN) zamanda çalışır.

 

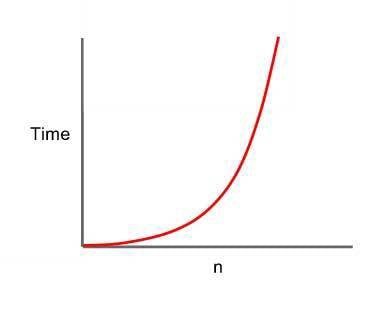
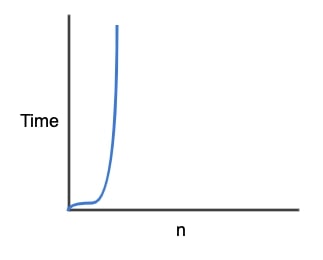
6) Üstel Karmaşıklık-O(2^N)

Üstel karmaşıklık (2 tabanında) logaritmanın tersi şekilde işlem sayısı üstel olarak algoritmalarda görülür.

İşlem açısından katlanarak artan bu tip fonksiyonlar sisteminizi tüketir.

• O(2^N) zamanda çalışır.

Kaynak: https://www.serkanseker.com/tr/wp-content/uploads/2021/09/Ustel-Big-O-Karmasikligi.jpg

 

7) Faktöriyel Karmaşıklığı-O(N!)

Faktöriyel, kendisinden küçük tüm pozitif tam sayıların çarpımıdır. Dolayısıyla faktöriyel karmaşıklığa sahip algoritmaların karmaşıklığı oldukça hızlı büyür.

• O(N!) zamanda çalışır.

 

En Hızlı Fonksiyondan En Yavaş Fonksiyona

 

1 -> logn -> n -> n.logn -> n² -> n³ -> 2ⁿ -> n!

 

Big-O Notasyonu Hesaplama Kuralları

• Döngüler: Bir döngünün çalışma zamanı döngü sayısının bir c sabitiyle çarpımı kadardır. Ancak, eğer bir döngünün n değeri sabit verilmişse. Örneğin: n = 100 ise değeri O(1)’dir.

• İç-içe döngüler: İçten dışa doğru her döngünün çalışma sayısı dıştaki döngü ile çarpılırken, sabit değerler de çarpıma dahil edilir.
• Ardışık ifadeler: Her bir ifadenin zaman karmaşıklığı eklenerek tek bir fonksiyon elde edilir.
• Logaritmik karmaşıklık: Bir algoritma, problemin çözüm kümesini belli sabit oranında bölüyorsa(örneğin ½ oranında), O(logn) şeklinde gösterilir.

 

Kaynakça

https://birhankarahasan.com/algoritma-analizi-nedir-zaman-karmasikligi-big-o-gosterimi

https://www.serkanseker.com/tr/algoritmalarda-big-o-gosterimi-big-o-notation/

 

Alıntıdır